Mega ciao!
La forza di gravità, oltre a tenerci ancorati alla Terra, descrive le orbite dei pianeti attorno al Sole. Le leggi del moto dei pianeti sono state enunciate dall’astronomo tedesco Giovanni Keplero ed hanno successivamente trovato conferma nella teoria della gravitazione universale di Newton. Ma cosa dicono le tre leggi?
1 – i pianeti orbitano attorno al Sole secondo un’orbita ellittica di cui la nostra stella occupa uno dei fuochi;
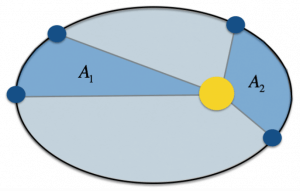
2 – il raggio vettore che collega il pianeta al Sole spazza aree uguali in tempi uguali. Nell’immagine qui sotto le aree A(1) e A(2) sono uguali. Questo significa che visto che in A(2) il pianeta deve percorrere un tratto di orbita più lungo rispetto a quando si trova in A(1), in A(2) dovrà andare più veloce. Dunque la velocità del pianeta varia a seconda del punto in cui si trova;
3 il quadrato del periodo di rivoluzione, P, (cioè il tempo che il pianeta impiega per compiere un’orbita completa) del pianeta attorno al Sole è proporzionale al cubo del semiasse maggiore, a, dell’orbita: P^2 = k*(a^3). La cosa interessante è che la costante di proporzionalità k è uguale per tutti i pianeti. Questo ci dice quindi che più grande è il semiasse maggiore dell’orbita, più lungo sarà il periodo di rivoluzione del pianeta.
Per esempio, la Terra, che ha un semiasse maggiore dell’orbita di circa 150 milioni di km, ha un periodo di rivoluzione di circa 365 giorni. Mercurio, che si trova molto più vicino al Sole rispetto alla Terra (con un semiasse maggiore di circa 58 milioni di km), impiega solo 88 giorni a compiere un’orbita attorno al Sole (quindi Babbo Natale ci mette molto meno tempo a tornare). Invece Saturno, che è molto più lontano (circa 1 miliardo e 433 milioni di km), impiega 10756 giorni (ovvero 29,45 anni…insomma qui è meglio non trasferirsi altrimenti Babbo Natale ci mette troppo tempo a ripresentarsi con il suo mitico sacco pieno di regali).
Ora siamo pronti per affrontare la teoria della gravitazione universale.
To be continued….
Sara