Mega ciao!
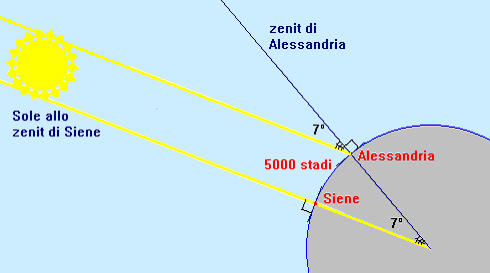
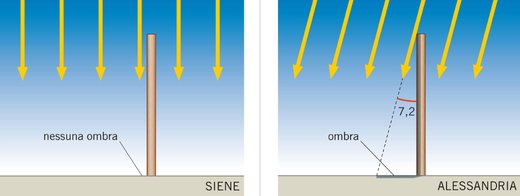
Torniamo ad Eratostene ed alla misura della circonferenza terrestre. L’astronomo arrivò al risultato grazie all’osservazione delle posizioni del Sole, accorgendosi che nel giorno del solstizio d’estate nella città di Syene il Sole non faceva alcuna ombra. Questo si può verificare costruendo un pozzo: il pozzo viene completamente illuminato, quindi il Sole passa allo zenith della città (cioè esattamente sopra la vostra testa). Nello stesso momento, ad Alessandria, situata circa 5000 stadi più a nord, sullo stesso meridiano di Syene, l’ombra prodotta dal Sole su uno gnomone indica che la distanza angolare tra la nostra stella e lo zenith è di 7°12′, cioè 1/50 di circonferenza. Quindi sapendo che le due città si trovavano sullo stesso meridiano, che la loro distanza lineare era di 5000 stadi e che quella angolare era 1/50 di circonferenza, questa rappresentava 1/50 di circonferenza terrestre, che risulta essere quindi di 250000 stadi, che sono stati arrotondati a 252000 stati per far corrispondere la lunghezza d’arco di 1° alla cifra tonda di 700 stadi. Ma a quanto corrisponde la lunghezza dello stadio di Eratostene? Ci sono due diverse versioni:
1- secondo l’astronomo Schiaparelli, famoso per aver mappato Marte, Eratostene ha usato lo stadio olimpico, lungo 183,75 metri. Questo corrisponde ad una circonferenza di
C=183,75×252000=46116000 m=46116 km,
cioè ad un raggio terrestre di
r=C/2 π=7339,6 km.
2- secondo Plinio, Eratostene usò uno stadio di 157,5 m, che corrisponde ad una lunghezza del meridiano di 39690 km, cioè ad un raggio terrestre di 6316,9 km.
Se teniamo valide le misure riportate da Plinio, ci accorgiamo che il raggio trovato si discosta da quello reale solo di 54,1 km. Insomma già due secoli prima della nascita di Cristo, gli astronomi sapevano che la Terra è sferica e sono riusciti a calcolarne il raggio e la circonferenza con una precisione quasi assoluta con gli scarsi strumenti che avevano all’epoca.
A presto!
Sara