Category: Approfondimenti

Mega ciao!

Volete partire per un viaggio spaziale? Iscrivetevi al nostro Corso Base di Astronomia Online in partenza il 26 ottobre. Durante le 8 lezioni vi porteremo dalla Terra ai confini dell’Universo, passando per attraverso il Sistema Solare, ammassi stellari, nebulose , galassie e spaghettizzandoci all’interno dei buchi neri. Per informazioni scrivetemi su messenger o su whatsapp al numero 3290689207. Per iscrivervi inviate al più presto una mail all’indirizzo

astrofilidischio@gmail.com

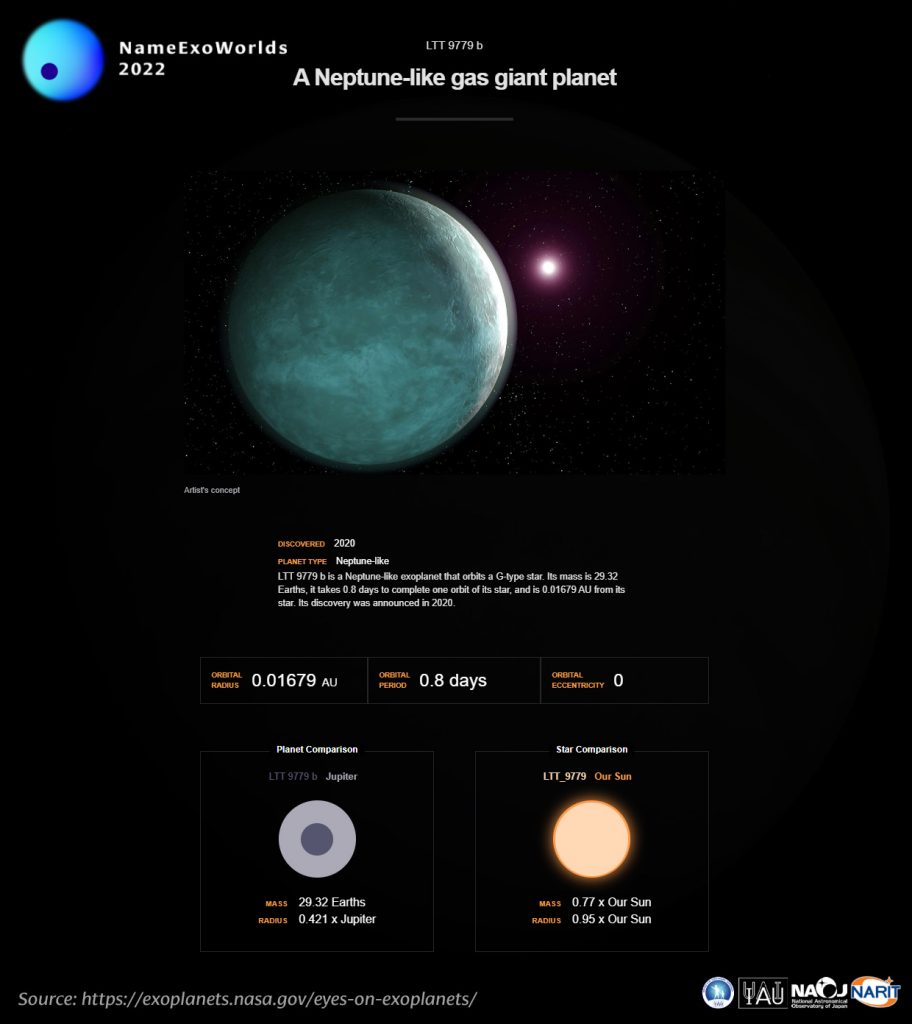
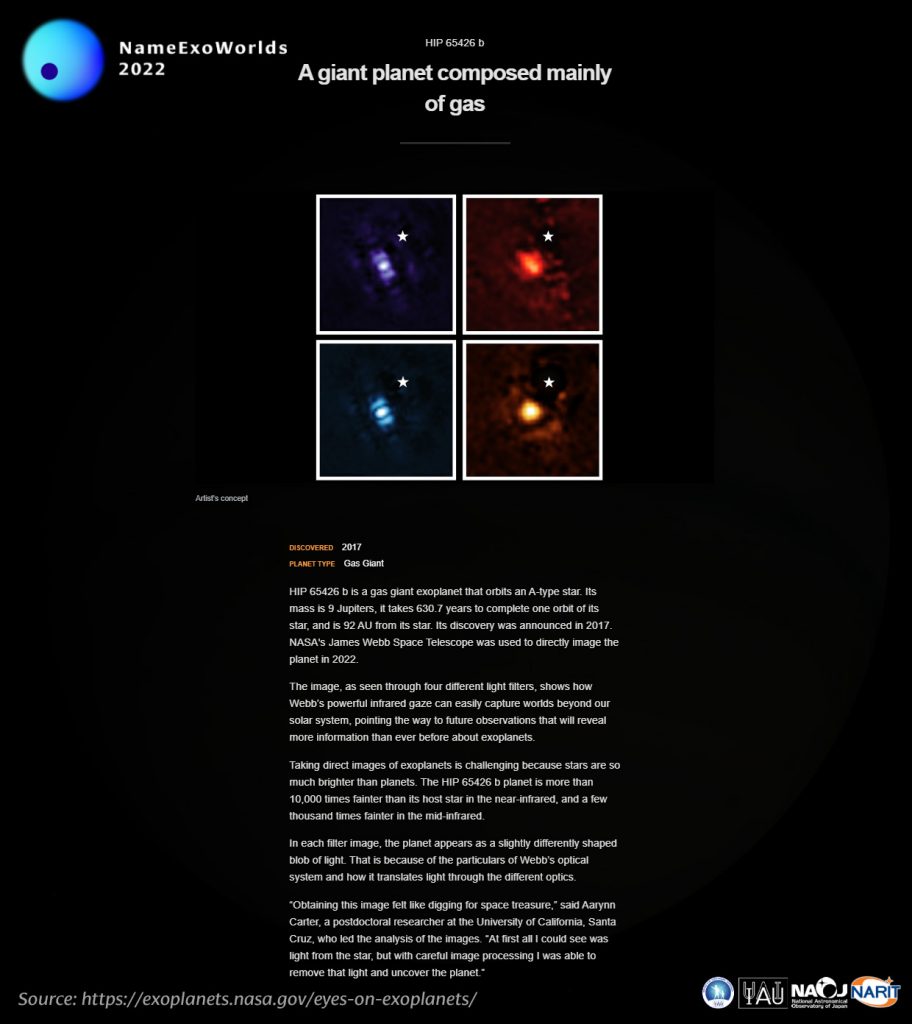
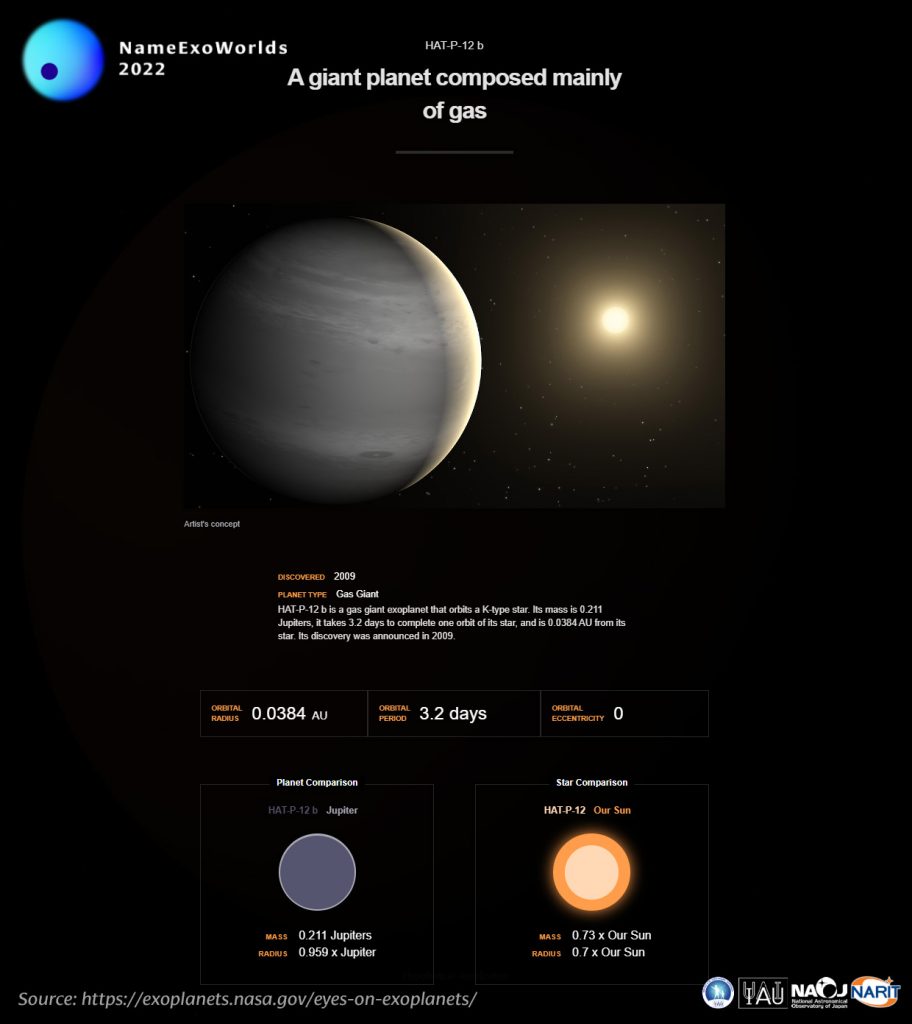
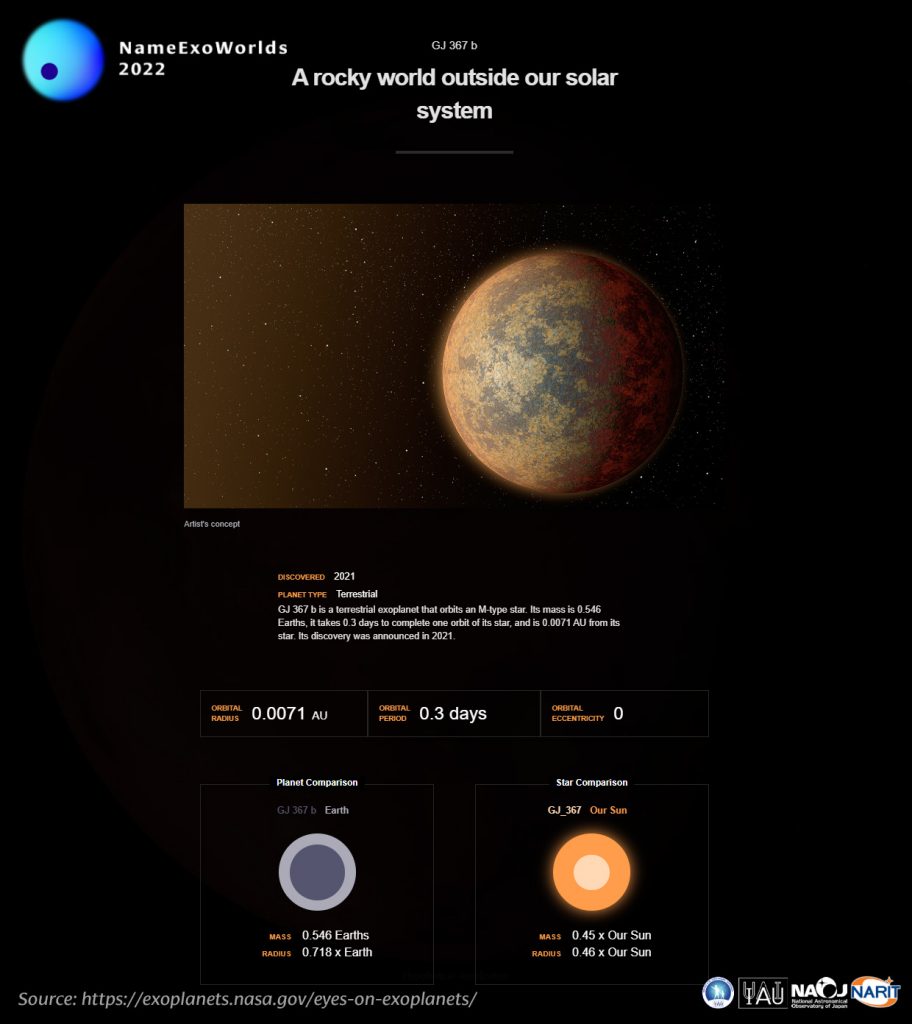
Vi ricordo inoltre che avete tempo fino all’11 dicembre per partecipare al concorso NameExoWorlds. Nel caso di LTT 9779 b il gatto che saltella sulla tastiera si è proprio impegnato. Questo esopianeta di tipo nettuniano ha una massa di 29.32 masse terrestri e un raggio di 0.421 raggi gioviani. La sua orbita è talmente stretta che viene percorsa in soli 0.8 giorni terrestri. Volete dargli un bel nome?

Formate un gruppo di due o più persone e scatenate la vostra fantasia partecipando al concorso NameExoWorlds. Trovate tutte le informazioni e le regole per la scelta dei nomi nel sito qui sotto.

A presto!

Sara

Name ExoWorlds

Mega ciao!

Ultimi posti disponibili al nostro Corso Base di Astronomia Online in partenza il 26 ottobre. Non lasciatevi scappare l’opportunità di partire con noi per un fantastico viaggio alla scoperta dell’Universo. Per informazioni scrivetemi su messenger o su whatsapp al numero 3290689207. Per iscrivervi inviate una mail all’indirizzo astrofilidischio@gmail.com al più presto.

Vi informo inoltre che l’IAU ha deciso di posticipare la scadenza del concorso NameExoWorlds. Avete tempo fino all’11 dicembre per partecipare. Uno dei pianeti disponibili è HIP 65426 b, un gigante gassoso in orbita attorno ad una stella di tipo A, situata nella costellazione del Centauro a circa 385 anni luce di distanza. Il pianeta ha una massa di 9 masse gioviane e si trova su un’orbita avente un semiasse maggiore di 92 unità astronomiche (circa 13.8 miliardi di chilometri). Il periodo orbitale è lunghissimo: circa 630.7 anni terrestri. HIP 65426 è importante in quanto è stato il primo esopianeta di cui il James Webb Space Telescope ha ottenuto un’immagine diretta. Volete dargli un bel nome?

Leggete bene il regolamento che trovate nel sito qui sotto e scatenate la vostra fantasia!

A presto!

Sara

Name ExoWorlds

Mega ciao!

Ultimi posti rimasti per partecipare al nostro Corso Base di Astronomia Online in partenza il 26 ottobre. Per informazioni scrivetemi su messenger o su whatsapp al numero 3290689207. Per iscrivervi inviate al più presto una mail all’indirizzo

astrofilidischio@gmail.com

Vi avviso che l’IAU ha deciso di posticipare all’11 dicembre la scadenza per partecipare al concorso NameExo Worlds.

Uno dei pianeti a cui potete decidere di dare un bel nome è HAT-P-12 b, un gigante gassoso con una massa di circa 0.211 masse gioviane e dimensioni simili a quelle di Giove. Situato nella costellazione dei Cani da Caccia a circa 468 anni luce di distanza da noi, il pianeta orbita attorno ad una stella di tipo K in appena 3.2 giorni terrestri. Volete dargli un nome che non sembri scritto da un bambino di un anno che batte le mani sulla tastiera del computer? Nel sito qui sotto trovate tutte le regole per partecipare al concorso.

A presto!

Sara

Name ExoWorlds

Mega ciao!

CHI VUOL ESSERE IMPERATORE DELL’IMPERO GALATTICO: SOLUZIONE E CLASSIFICA

Vi avevo chiesto dove iniziano i processi di formazione stellare. Le risposte giuste sono: in una regione di una nube molecolare a bassissima temperatura e con una massa superiore a 1000 masse solari (risposte a e b). Analizziamo prima le due opzioni sbagliate. La c non è corretta in quanto le nebulose planetarie si formano dalla morte di stelle simili al Sole e il loro materiale tende ad espandersi e a dissolversi nello spazio interstellare. La d è sbagliata perchè le nubi molecolari da cui si formano le stelle hanno una densità molto bassa: tra le 10 e le 300 molecole/cm^3. L’atmosfera terrestre invece ha una densità di circa 27 miliardi di miliardi di molecole al centimetro cubo. Le stelle si formano a seguito di eventi catastrofici che sconvolgono l’equilibrio di una nube molecolare, come l’onda d’urto proveniente dall’esplosione di una supernova vicina o lo scontro con un’altra nebulosa. Per poter formare una stella, la regione della nube coinvolta nella perturbazione deve avere una massa superiore alle 1000 masse solari (massa limite di Jeans). Inoltre, le nubi molecolari hanno una temperatura molto bassa: da 10 a 100 K. Adesso mi direte che 100 gradi è una temperatura alta, ma attenzione che parliamo di gradi Kelvin. Facendo la conversione, queste due temperature corrispondono rispettivamente a -263.15 e a -173.15°C.

Qui sotto trovate la classifica. Come al solito se avete fornito due risposte di cui una sbagliata avete preso zero punti. Domenica giocherete per 3000 crediti galattici. Se avete sbagliato risposta non demoralizzatevi: siete ancora in corsa per la conquista dell’Impero Galattico (vi ricordo che i punti corrispondenti ad ogni risposta giusta che date vengono sommati). Continuate a giocare con noi!

Vi ricordo inoltre che ci sono ancora posti al nostro Corso Base di Astronomia Online in partenza il 26 ottobre. Per informazioni scrivetemi su messenger o su whatsapp al numero

3290689207.

Per iscrivervi inviate una mail all’indirizzo

astrofilidischio@gmail.com

A presto!

Sara

Mega ciao!

Vi ricordo che avete tempo fino al 10 ottobre per iscrivervi al nostro Corso Base di Astronomia Online. Le 8 lezioni si terranno su Zoom ogni mercoledì sera alle ore 21:00 a partire dal 26 ottobre. Per informazioni scrivetemi su messenger o su whatsapp al numero 3290689207. Per iscrivervi inviate una mail all’indirizzo astrofilidischio@gmail.com

Torniamo a parlare di NameExoWorlds. Il secondo pianeta a cui potete dare un nome è GJ 436b, situato nella costellazione del Leone a circa 33 anni luce di distanza da noi. Ha dimensioni simili a quelle di Nettuno, ma si trova su un’orbita molto più stretta: Babbo Natale passa ogni 2.6 giorni terrestri. La sua particolarità? Sembra che non abbia metano, una cosa stranissima per un pianeta con una temperatura di 800 K. Volete dargli un bel nome?

Avete tempo fino all’11 novembre per partecipare al concorso NameExoWorlds! Trovate tutte le informazioni nel link qui sotto.

A presto!

Sara

Name ExoWorlds

Mega ciao!

Vi ricordo che avete tempo fino all’11 novembre per partecipare al concorso NameExoWorlds. All’Unione Astronomica Internazionale serve il vostro aiuto per dare bei nomi a 20 sistemi planetari. La cosa fantastica questo giro è che tutti questi sistemi saranno presto analizzati dal James Webb Space Telescope. Come sono fatti?

Il primo, GJ367b, situato nella costellazione della Vela, è unpianeta terrestre con una massa circa la metà di quella della Terra. Orbita attorno ad una stella più piccola del Sole in appena 0.3 giorni terrestri. Questo significa che lì Babbo Natale passa ogni 0.3 giorni. Per farvi un confronto, Mercurio (il pianeta più vicino al Sole) ha un periodo orbitale di circa 88 giorni terrestri. Trovate tutte le info per partecipare al concorso nel sito qui sotto. Volete saperne di più sugli esopianeti?

Iscrivetevi al nostro Corso Base di Astronomia Online in partenza il 26 ottobre. Per informazioni scrivetemi su messenger o su whatsapp al numero 3290689207. Per iscrivervi inviate una mail all’indirizzo astrofilidischio@gmail.com entro il 10 ottobre.

A presto!

Sara

Name ExoWorlds

Mega ciao!

CHI VUOL ESSERE IMPERATORE DELL’IMPERO GALATTICO: SOLUZIONE E CLASSIFICA

Vi avevo chiesto quale tra le affermazioni proposte sui pianeti extrasolari fosse corretta. Le risposte esatte sono: alcuni sono stati osservati con immagini dirette e possono essere talmente caldi da presentare piogge di ferro (risposte a e d). Analizziamo innanzitutto le due sbagliate. La b non è corretta perchè la tecnica più produttiva nella scoperta degli esopianeti non è quella delle velocità radiali, ma quella dei transiti. Infatti, ad oggi i pianeti scoperti con la tecnica delle velocità radiali sono 1012, mentre con i transiti ne sono stati individuati 3900. La risposta c è sbagliata perchè l’unico candidato esopianeta scoperto in un’altra galassia è stato individuato grazie alla curva di luce in banda X, non nell’ottico. Per quanto riguarda le due risposte giuste, gli esopianeti osservati con immagini dirette sono 61 (pensate che uno è stato osservato poco tempo fa dal James Webb Space Telescope) e su WASP 76b, un bel gigante gassoso, è così caldo che piove ferro.

Nell’immagine trovate la classifica. Come al solito chi ha dato entrambe le risposte giuste ha preso punteggio pieno, chi ha fornito una risposta giusta e una sbagliata ha preso 0 punti, mentre chi ha indicato una sola delle varie opzioni ma corretta ha preso metà punti. Domenica giocherete per 2000 crediti galattici.

Vi ricordo che, fino ad esaurimento posti, sono aperte le iscrizioni al nostro Corso Base di Astronomia Online in partenza il 26 ottobre. Per informazioni scrivetemi su messenger o su whatsapp al numero 3290689207. Per iscrivervi inviate una mail all’indirizzo astrofilidischio@gmail.com entro il 10 ottobre.

A presto!

Sara

Mega ciao!

CHI VUOL ESSERE IMPERATORE DELL’IMPERO GALATTICO: SOLUZIONE E CLASSIFICA

Vi avevo chiesto quanti dovrebbero essere i pianeti abitabili nella Via Lattea secondo un recente studio basato sui dati di Kepler. La risposta corretta è: 300 milioni (risposta d). Kepler è stato un telescopio spaziale con l’unico obiettivo di cercare pianeti extrasolari monitorando la luminosità di circa 148000 stelle situate tra le costellazioni della Lira, del Cigno e del Drago. Statisticamente parlando, basandoci sui dati di questa missione troviamo che considerando pianeti con un raggio compreso tra 0.5 e 1.5 raggi terrestri, orbitanti attorno a stelle simili al Sole, i pianeti abitabili sono 300 milioni. Nell’immagine potete vedere la classifica. Domenica giocherete per 1500 crediti galattici.

Se volete saperne di più sui pianeti extrasolari vi ricordo che sono aperte, fino ad esaurimento posti, le iscrizioni al nostro Corso Base di Astronomia Online. Per informazioni scrivetemi su messenger o su whatsapp al numero 3290689207. Per iscrivervi inviate una mail all’indirizzo astrofilidischio@gmail.com entro il 10 ottobre.

A presto!

Sara

Mega ciao!

Negli anni ’60 un contatore Geiger lanciato a bordo di un razzo ha rivelato radiazione in banda X proveniente dalla costellazione del Cigno. Questo segnale è stato studiato sistematicamente negli anni ’70, fino alla scoperta delle sue controparti radio e ottica. La sorgente Cygnus X-1, situata a circa 6197 anni luce di distanza da noi, è situata in un sistema binario. Orbita attorno alla stella supergigante blu HDE 226868 in circa 5.6 giorni terrestri. Dallo studio dell’emissione X è risultato che la sorgente è variabile su scale temporali di millisecondi. Questo significa che il suo diametro è minore di qualche centinaio di chilometri. Che sia una stella di neutroni o un buco nero?

Dai parametri orbitali combinati con l’emissione alle diverse lunghezze d’onda è risultato che la massa dell’oggetto invisibile è di circa 14.8 masse solari. Un oggetto con una massa così grande confinata in uno spazio così piccolo può essere solo un buco nero. Volete saperne di più?

Parleremo un sacco di buchi neri durante il nostro Corso Base di Astronomia Online in partenza a fine ottobre. Le 8 lezioni si terranno su Zoom ogni mercoledì sera alle ore 21:00 a partire dal 26 ottobre. Per informazioni scrivetemi su messenger o su whatsapp al numero 3290689207 (NON risponderò a chiamate normali). Per iscrivervi inviate una mail all’indirizzo astrofilidischio@gmail.com entro il 10 ottobre. Le iscrizioni sono aperte fino ad esaurimento posti.

A presto!

Sara

Mega ciao!

Avete presente le immagini spettacolari delle galassie riprese dal telescopio spaziale Hubble? Ai tempi di Hubble (Edwin, non il telescopio) non esistevano tutte le belle foto colorate che ci sono oggi. Gli astronomi lavoravano su lastre fotografiche, come quella che vedete qui. Questa è la galassia NGC 3115, situata nella costellazione del Sestante a circa 32 milioni di anni luce di distanza da noi. Dalle lastre fotografiche può risultare molto difficile determinare il tipo morfologico dell’oggetto osservato. Che sia una galassia ellittica o lenticolare? Quali sono i tipi morfologici delle galassie e come possiamo distinguerli?

Lo potrete scoprire durante il nostro Corso Base di Astronomia Online in partenza quest’autunno. Le 8 lezioni si terranno su Zoom ogni mercoledì sera alle ore 21:00 a partire dal 26 ottobre. Per informazioni scrivetemi su messenger o su whatsapp al numero 3290689207 (NON risponderò a chiamate normali). Per iscrivervi inviate una mail all’indirizzo astrofilidischio@gmail.com entro il 10 ottobre. Iscrizioni aperte fino ad esaurimento posti.

A presto!

Sara