Mega ciao!
Passato bene il weekend?
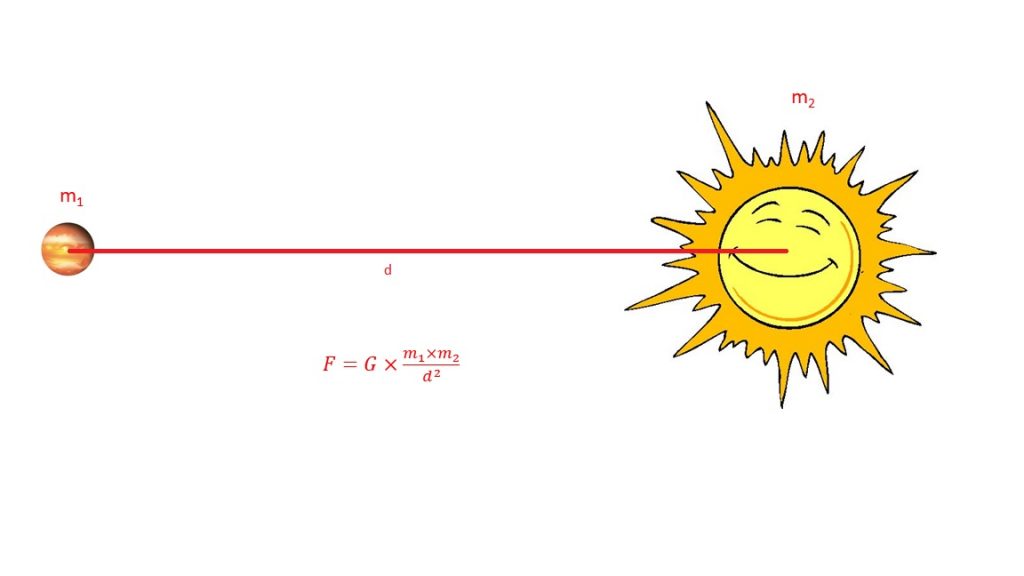
Abbiamo visto le tre leggi di Newton e la scoperta della forza di gravità. Il buon Sir Isaac però ha fatto un passo in più: ha determinato la forza con cui due corpi dotati di massa si attraggono nello spazio. Questa forza è descritta dalla legge di gravitazione universale. Consideriamo due oggetti nello spazio: Giove, che ha una massa mG, e il Sole, che ha una massa MS. Giove e il Sole sono separati da una distanza r. Newton ci dice che la forza con cui Giove e il Sole si attraggono è
Fg = G * mG * MS / r2
dove G è la costante di gravitazione universale e vale 6.67*10-11 N m2 / kg2.
Cosa ci dice questa formula?
La forza con cui si attraggono due oggetti massicci nello spazio è direttamente proporzionale al prodotto tra le masse dei due oggetti ed è inversamente proporzionale al quadrato della loro distanza. In pratica, questa forza sarà molto più intensa nel caso di oggetti molto massicci e molto vicini. La forza diventerà più debole man mano che ci allontaniamo dall’oggetto considerato. Cosa ne dite se facciamo quattro conti? Giove e il Sole hanno una massa rispettivamente di circa 1.898*1027 kg e 1.989*1030 kg. La distanza media tra loro è di 778340821 km. Inseriamo questi numeri nella formula per trovare la forza di gravitazione (ricordandoci di convertire la distanza in metri per rendere le misure compatibili!!!). La forza risulta:Fg = 4.16*1023 N.Cosa succede se spostiamo Giove più vicino al Sole? Prendiamo il pianeta gigante e mettiamolo al posto di Mercurio. In questo caso la distanza media dal Sole è di 57909227 km. La forza di gravitazione risulta quindi:
Fg = 7.5*1025 N.
E se lo spostiamo alla distanza di Proxima Centauri? In questo caso r = 4.246 anni luce = 4.017*1013 km. La forza risulta quindi:
Fg = 1.56*1014 N.
Vedete quindi come diminuire la distanza faccia aumentare la forza con cui i due oggetti si attraggono, mentre aumentare la distanza significa diminuire drasticamente la forza.
A presto!
Sara