Mega ciao!
CHI VUOL ESSERE IMPERATORE DELL’IMPERO GALATTICO: SOLUZIONE E CLASSIFICA
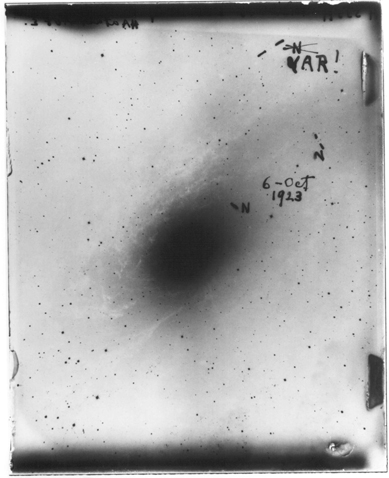
Vi avevo chiesto quale processo fornisce energia alle stelle di cinque masse solari durante la fase principale. La risposta corretta è: il bruciamento dell’idrogeno tramite il ciclo carbonio – azoto – ossigeno (risposta B). La fase principale corrisponde alla linea diagonale che va da in basso a destra a in alto a sinistra nel diagramma di Hertzsprung – Russel. In questa fase la stella brucia idrogeno tramite reazioni nucleari. La durata e il processo con cui avviene il bruciamento dipende però dalla massa della stella. Nel caso del Sole il bruciamento nucleare avviene tramite la catena protone – protone, con cui quattro atomi di idrogeno vengono fusi in un atomo di elio tramite una catena di reazioni. Perchè serve una catena di reazioni?
In natura gli scontri tra più di due particelle sono altamente improbabili, di conseguenza è impossibile che quattro atomi di idrogeno si scontrino contemporaneamente e si fondano in un atomo di elio. Succede la stessa cosa in stelle di cinque masse solari?
Non proprio. Stelle così massicce raggiungono temperature molto più elevate rispetto al Sole e bruciano quindi l’idrogeno tramite il ciclo carbonio – azoto – ossigeno (CNO cycle). In questo caso abbiamo sempre quattro atomi di idrogeno che vengono fusi per formare l’elio, ma la reazione è catalizzata da carbonio, azoto e ossigeno. Le reazioni sono quindi totalmente diverse rispetto a quelle della catena protone – protone. Il ciclo carbonio – azoto – ossigeno comincia a dominare le reazioni nel nucleo a partire da stelle di 1.5 masse solari.
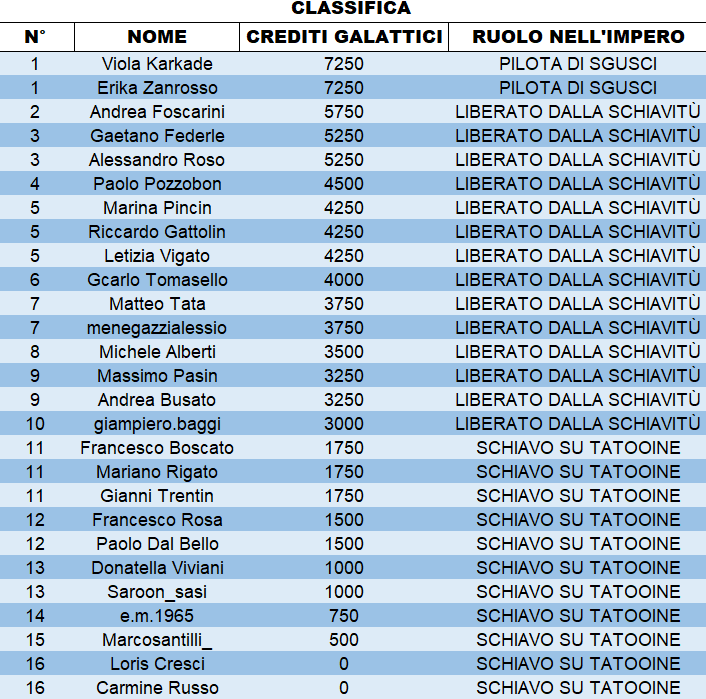
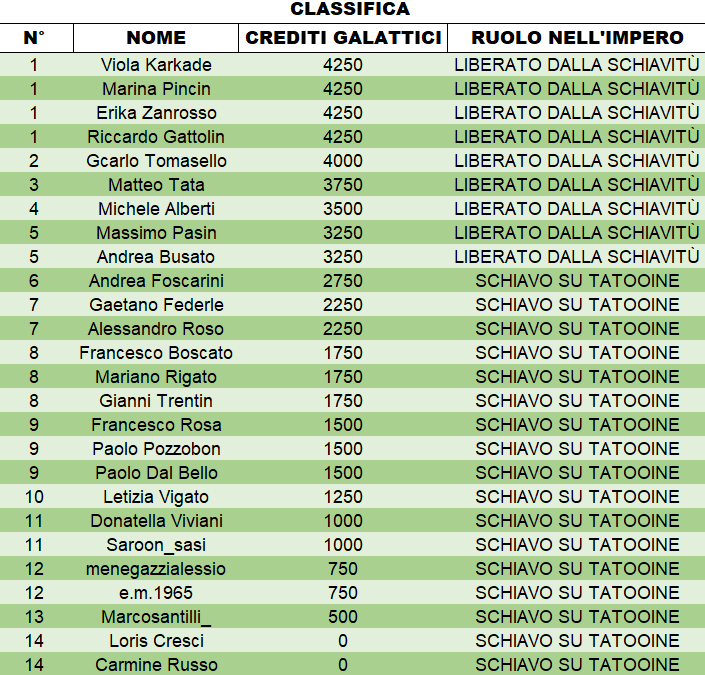
Qui sotto trovate la classifica. Alcuni di voi sono diventati piloti alle gare degli sgusci, mentre altri sono riusciti a liberarsi dalla schiavitù. Lunedì prossimo giocherete per 5000 crediti galattici.
Vi ricordo che avete tempo fino al 15 febbraio per iscrivervi al nostro Corso Avanzato di Astronomia Online. Per informazioni chiamatemi al numero
3290689207.
Per iscrivervi inviate una mail all’indirizzo
astrofilidischio@gmail.com
A presto!
Sara